An Guide to Two's Complement from a Set Theoretical Perspective:
Part 1
Introduction
The ability of computers to rapidly and accurately perform extremely complex mathematical calculations is a convenience that we often take for granted. Mathematical computations are used by the computer graphics libraries that allow us to use software with graphics, such as modern video games with stunning visuals. Complex mathematical calculations are also involved in encrypting data that we send over the internet, such as credit card numbers, when performing secure online transactions such as purchases or bill payments in a way that prevents identity theft. Behind the scenes, underlying all of these seemingly magical capabilities, there lies a complex framework of carefully engineered circuits performing logical operations for our benefit.In this post, I will attempt to demystify a small part of process by which computers perform mathematical calculation by answering a deceptively simple-sounding question: How do computers represent negative numbers?
Background: Basics of Set Theory
In order to avoid misleading and hand-wavy answers to the question of interest, we need to first explore some fundamental mathematical concepts that are extremely useful in this context. In particular, a few basic ideas from set theory are extremely valuable tools when trying to understand how math is performed on computers.First, we need to introduce the concept of a set. A set is a mathematical abstraction for a grouping of some items. A common analogy used to describe sets is that a set is like a bag that contains some collection of objects. This is a useful analogy because it captures the essence of what a set is while also illustrating some of the more confusing properties of sets. For example, the empty set, a set which contains nothing, is denoted by the following symbol:
A set is also often denoted by curly braces; that is, the set begins with the symbol "{" and ends with the symbol "}", and the items in the set are separated by commas. Using this convention, an empty set can also be represented by:
These two symbolic representations are equivalent and interchangeable. Note, however, that the empty set is not equivalent to a set containing the empty set:
The bag analogy illustrates this nicely. Obviously, an empty bag is not physically the same thing as a bag containing another empty bag. For similar reasons, a set containing the empty set is not empty.
Not every set is empty. In fact, there are infinitely many different examples of sets that are not empty. To give an example of what one of these would look like, we can consider the set of digits that we use to represent numbers in base 10 (this set is also sometimes called the integers modulo 10):
So much for sets. Now, we need to introduce a related concept called the relation. A relation is a mathematical construct used to represent certain kinds of relationships between two sets. A relation can represented visually by graphs (often used in algebra) or arrow diagrams (often used in philosophy and logic). A relation between two sets is always a relation from one set to another set.
For example, the ASCII table (http://www.asciitable.com/), a tool widely used in programming in the convenient use cases where one does not have to fiddle with Unicode character sets, represents multiple relations in an extremely compact form. One of these relations is a relation between the integers and the letters of the alphabet. This relation can be represented by the following arrow diagram:
One special way of looking at a relation is to consider it as mapping both to and from the same set. In some cases, this perspective comes more naturally than in others. For example, victory conditions in the classic non-transitive game Rock, Paper, Scissors can be represented by such a relation, where each item is mapped to the choice that it beats:
If you picked a given choice in the left circle above, you would win against the choice in the right circle pointed to by the arrow leading out of your choice. Another way of representing a relation is as a set of ordered pairs, where the first element in each pair is from the domain, and the second element in each pair is from the codomain. The pairs that are present in the relation are exactly those pairs of elements connected by arrows in an arrow diagram. For example, the victory conditions in the game Rock, Paper, Scissors can be represented as the following set:
Although every relation has an inverse, not every function has an inverse, because we define the inverse of a function to be a functional relation that reverses the relationship in question.
This post introduced the basics of set theory. This topic will be continued in the next post, where we study some useful properties of relations, before we wrap up by applying set theory to the question of representing negative numbers on computers.
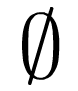


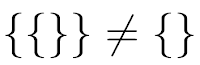


No comments:
Post a Comment