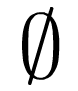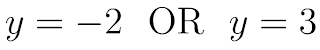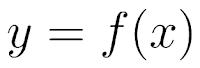The Egg Drop: Part 3

Induction

In the previous post, we used calculus to determine an optimal strategy for solving the egg drop problem with 2 eggs. Now, what if n = 3 (that is, we have had 3 eggs instead of 2)? In this case, we can split the building into a certain number of sections with the first egg, then split the section of interest into subsections with the second egg, and then explore the final subsection with the last remaining egg.

So, what is the optimal number of sections and subsections that we should split the building into? Note that this problem contains the problem for n = 2 within it! That is, once we have broken the first egg while splitting the building into a number of sections, we have determined a certain section to search with 2 remaining eggs. This problem is then identical to the one we solved above. This allows us to assume two useful properties. First, we know the number of subsections that we want within each section will be the equal to square root of the size of the section:

Secondly, we know that the size of the subsections will be the same as the number of subsections within one section. We know this because the number of subsections in one section times the size of each subsection equals the size of one section, and the number of subsections per section is the square root of the section size, so the subsection size must also be equal to the square root of the section size (if a*b = c, and a*a = c, then a = b)!

In the worst case, then, the number of trials performed with the second egg will be equal to the number of drops performed with the third egg. (Actually, in determining the section if interest, we also test one of the floors in that section, so the third egg will have 1 less trial, just as the second egg in the n = 2 case had 9 drops vs. the 10 drops with the first egg. This discrepancy is not asymptotically significant, so we ignore it). Using these assumptions, we can create an expression for T, the total number of worst-case trials performed:

By setting the derivative equal to 0, we can solve for the optimal s₀ (number of sections created with the first egg):

Are you noticing a pattern here? When we have n eggs, the best strategy is to split the area of interest into x sections at every step, where x*x = n. The worst case number of trials will be the same for each egg, because we want to use each egg to its full potential in order to minimize the total number of trials. This can be proven rigorously using induction. The steps are almost identical to the derivation for 3 eggs above. We assume in the induction hypothesis that the last n-1 eggs all have an equal number of trials in the worst case, and that this number is equal to the rth root of h/s₀, where r = n -1. Then, the induction step, which is again almost identical to the derivation above, demonstrates that s₀ must be equal to the nth root of h. It follows very straightforwardly from this that all the other eggs also have an equal number of worst case trials.

Is this analysis even worth doing, even from a theoretical standpoint? It is easy to show that with n eggs, the worst case number of trials is equal to:

The actual number of worst case trials may be bounded by this plus some small constant (1?), but this is irrelevant for asymptotic analysis. The important point is that for some fixed number n of eggs, the worst case run time is bounded (big Theta) by the nth root of h, where h is the number of floors. Since different roots have different asymptotic growth, each additional egg actually provides an asymptotically significant advantage, making the run-time grow more slowly with the size of the input (number of floors of the building) from an asymptotic point of view.

There is, however, a limit to the benefits of using additional eggs. Once the number of eggs, n, reaches the log base 2 of the number of floors lg(h), we are splitting the building into 2 sections at every step. There is no algorithm more efficient than this, and adding additional eggs provides no additional benefit once n is greater than or equal to lg(h). We cannot split the building into fewer than 2 sections; treating it as 1 section would take us back to the naive strategy that is optimal for 1 egg, which is never efficient with more eggs.

That's it for this post! I hope you enjoyed the weird mix of calculus and induction.

The Egg Drop: Part 2

Using Calculus

Previously, I introduced the egg drop problem. Now, we will apply calculus to help optimize our algorithm.

The trick here is to model the total number of drops as a mathematical function. Notice that the general approach described above is to use the first egg to "split" the building into a certain number of equally sized sections, and test these sections from the bottom up. Once you know which section the desired floor lies in, we can use the second egg to pinpoint the exact floor.

In the worst case scenario, where the desired floor is the second highest floor, the total number of trials we perform with the first egg is equal to the number of sections we are splitting the building into. For example, if we split the building into 2 sections, we would drop the first egg from the middle floor and it would remain unbroken; then, we would drop it from the top floor and it would break, so we would have to work our way up with the second egg.

So the first egg undergoes at most s drops, where s is the number of sections we are dividing the building into. The size of any given section of the building is then h/s. Notice that we may have to test the entire section once the first egg breaks; to be safe, we have to start the second egg from the bottom of the given section and work our way up. Therefore, the second egg undergoes at most h/s drops.

Hence, we can represent the total number of trials in the worst-case scenario as a function of the number of sections we choose to divide the building into according to our strategy:

We want to minimize T, the number of trials, by choosing an optimal number of sections to divide the building into by dropping the first egg at certain intervals. The easiest way to determine the optimal value for s to minimize T is to take the derivative of the expression above and set it equal to zero. As always, calculus is great for optimization.

A few caveats: in general, this approach could produce multiple solutions, which could be maxima as well as minima. Finally, optimization with calculus helps us to find local extrema, and the global minimum does not necessarily have to be a local minimum recognizable by differentiation (it could be one of the endpoints of the domain). Finally, this problem, like most algorithmic problems, is discrete by nature, whereas calculus relies on differentiability. If calculus instructs us to split the building into pi/2 sections, then we might be in trouble, because we have only integer numbers of floors to work with. Nevertheless, in this case, we will see that this approach is an extremely elegant way to determine the exact solution.

Differentiating the expression for total worst-case number of trails, we find:

When we set the derivative to zero, we find:

This indicates that the number of sections we should divide the building into is equal to the square root of the height of the building in floors. That is, for the 100 story building, we would start by dropping the first egg at floor 10, then floor 20, etc. Once the first egg broke, we would only have 9 floors remaining to test, so the worst case scenario is that the first egg breaks after 10 drops and then the second egg is dropped 9 times, for a total of 19 drops.

Actually, the optimal solution to this problem is slightly more complicated than the solution just described above. Suppose we drop the first egg at floor 10 and it doesn't break. Then, we have 2 eggs remaining and 90 floors. But, the math we just did shows that in such a scenario, the best strategy is to split the remaining floors into x sections, where x is the square root of the number of floors. The square root of 90 is approximately 9, so the best strategy would be to split the 90 remaining floors into 9 sections. We would begin by dropping at floor 20. Then, we would have 80 floors, which we would still want to split into approximately 9 sections. Therefore, we would next drop at floor 29, instead of floor 30! This is extremely confusing. For the purposes of this blog, we will not recalculate the optimal algorithm at every drop, even though from a purely theoretical standpoint that is more efficient (assuming that the actual climbing of stairs in the building and dropping of the egg is much more difficult and time-consuming than the calculation).

In this post, we saw how to use calculus to solve the case for n = 2. But, what if we have even more eggs? Is there some way to reuse our insights from the n = 2 case to derive a more general solution? In the next post, we will use induction to generalize our results. (I will not actually do rigorous induction, but I will give an example that will show the framework that could be used to prove the result by induction).

The Egg Drop: Part 1

Introduction

This post is about a famous algorithmic optimization problem. My goal with this post is to try to apply calculus to discrete mathematics in a useful way. For some calculus is almost totally ignored in algorithmic analysis, even though (I think) it can be quite useful! This problem will show how.

Assume you are given n eggs to experiment with, and a building with h floors. You're in a magical world without terminal velocity, so when you drop an egg from a window on a given floor, the higher the floor that you drop the egg from, the harder it will hit the ground. You are tasked with figuring out which floor of the building is the highest floor that an egg can be dropped from without breaking upon impact.

You need to come up with a strategy that will provide the answer to this question by the time you have used up all n eggs. An egg is used up once it is broken by dropping it from a floor that is too high. The challenge is to describe an algorithm that will produce the answer as quickly as possible. That is, in the worst case scenario, you should have to conduct as few trials as possible, where a single trial consists of dropping an egg out of a certain window and observing whether or not it breaks. We will approach this problem by beginning with 1 egg, and then gradually increasing the number of eggs provided and noticing what pattern develops.

When n = 1, the problem is trivial. Since you only have one egg and you can't risk breaking the egg without figuring out the exact floor, you need to start at the bottom of the building and work your way up, dropping the egg from every floor until it breaks. Once the egg breaks, you know that the floor below that is the highest safe floor. In the worst case, this will take h drops.

With n = 2, the problem is significantly more challenging. You could take the same approach as in the n = 1 case, but then you would have wasted the advantage of having 2 eggs. How can we be as efficiently as possible?

Suppose you start by dropping from halfway up the building. For example, if h = 100 (the building has 100 floors), then you would start by dropping an egg from the 50th floor. If this egg doesn't break, then you've saved yourself the trouble of even testing the bottom half of the building, because if the egg doesn't break from the 50th floor, it won't break from any of the lower floors! If the egg does break, you have 1 egg left and 50 floors, so you work your way up from the bottom. The farthest you could possibly have to go is floor 49, so the worst case scenario is 50 drops, or h/2. This is much better than the worst case of h drops with n = 1. Note that we can only take this shortcut because we have 2 eggs. If we only had 1 egg, and we dropped it from floor 50 and it broke, then we would have used up our eggs without solving the problem. That would be unacceptable.

So, we can do slightly better with 2 eggs, but is dropping from halfway up the building the best we can do? What if we drop the first egg from 1/3 of the way up? In a 100 story building, this would be about floor 33. If the egg breaks, the worst case is 33 drops, since we have 1 egg remaining to test the bottom 32 floors. If the egg doesn't break, we can drop from floor 66, and then floor 100. If the first egg breaks at floor 100, then we only have to test floors 67-99 with the second egg. The total number of drops in the worst case here is the 3 drops with the first egg plus 32 drops with the second egg, which is 35, even less than the 51 drops with the halfway strategy!

It seems from these examples like the smaller the interval at which we drop our first egg, the more efficient we are. But that can't be true in general, because if we just drop the first egg at every floor, we're back to 100 drops total, which is really bad! How can we figure out the optimal division of labor between the two eggs?

In the next post, we will see how we can use calculus to quickly determine the solution.

Principles of Machine Mathematics (Part 3 of 3)

An Guide to Two's Complement from a Set Theoretical Perspective:

Part 3

Binary Numbers

If you look back to the ASCII table (http://www.asciitable.com/) that we referenced in part 1 of this post, you will notice that in addition to columns containing the decimal integers and the symbols, there are columns for hexadecimal and octal representations of integers and HTML. The reason hexadecimal and octal codes are useful is because they translate easily into binary numbers, which much more directly represent the way that computers store information.

Every conceivable kind of information that a computer stores or manipulates is represented in bits, which correspond to the voltage in some part of some circuit being either "high" or "low" according to some pre-defined thresholds with respect to some consistent reference value. The highness or lowness of voltages is a 2-state system that is very naturally represented by 0's and 1's, the only two digits used to represent numbers in a binary numeral system. This is a vast enough topic that it makes no sense for me to cover it in detail in my blog; see Wikipedia for details (https://en.wikipedia.org/wiki/Binary_number). One characteristic of interest, though, is that with positive numbers in binary notation, addition with pencil and paper works the same way that it does for decimal numbers, where you start from the one's place and carry overflow to the next lowest place.

The Sign & Magnitude Convention

Because computer's can't directly store arbitrary symbols or concepts such as a negative sign, the most straightforward way to represent negative numbers is to use a single bit (which can be 1 or 0) to represent the sign of a number (+ or -), since both a bit and a sign can have two states. The simplest way to do this is the sign and magnitude convention for storing negative numbers, where the first bit represents the sign, and all subsequent bits represent magnitude.

Consider the set of 3-bit binary numbers, ranging from 000 to 111. If we consider the leading 0 to represent + and the leading 1 to represent -, and the remaining bits to represent magnitude, then 001 =  1, 101 = -1, and 110 = -2. But how did we choose which negative numbers to assign to which bit strings? We chose the negative numbers with the same absolute value as the positive numbers with the same bit string (disregarding the sign bit). Remember, though, that the absolute value relation is NOT arithmetic invariant! Indded, if we perform arithmetic by pencil and paper as we do with decimal numbers, 001 + 101 = 101, which means 1 + -1 = -2. This doesn't make any sense. To make matters worse, not only is arithmetic with the sign & magnitude convention not intuitive on paper, it also requires more complex circuitry for the same reasons. This is one of the major reasons that the sign & magnitude convention is almost never used in modern computer systems.

Ones' Complement 

In ones' complement, the first bit still indicates sign, but the trailing bits indicate magnitude only for positive numbers. For negative numbers, where the first bit is 1, the magnitude of the number is determined by flipping the trailing bits. For example, 101 has a magnitude of flip(01) = 10 = 2. Therefore, 101 = -2. Similarly, 110 has a magnitude of 01 = 1. Thus, even though 001 + 101 = 110, this means that -2 + 1 = -1 in ones' complement, which makes sense.

Why does this addition work so naturally in ones' complement? It's because ones' complement secretly relies on a modular congruence relation. Every negative number in ones' complement and the positive number that is represented by the same trailing bit string are in the same congruence class modulo x, where x equals (2 raised to the number of trailing bits) minus 1. With three bits, this magic number is 3. Notice that 1 % 3 = 1 = -2 % 3.

The main reason ones' complement is not the standard for representing negative numbers is that it allows for a representation of negative zero (111). This is unfortunate because checking if a value is equal to zero is an extremely common operation in computer programming, and in ones' complement systems this operation is slightly inefficient because one has to perform two checks instead of one, since there are two binary strings that represent 0: 000 and 111 (in our imaginary 3-bit system).

Two's Complement

Two's complement is extremely similar to ones' complement. The difference is that obtaining the magnitude of a negative number can be done by flipping the bits and then adding one, instead of just flipping the bits. This modification is done to ensure that even the most positive negative number (111) is equal to -1 instead of 0, ensuring that there is only 1 representation of 0. As a result of this, it is actually possible to store more negative numbers than positive numbers.

Two's complement also secretly relies on a modular congruence relation, the relation modulo (2 raised to the number of bits). In our 3 bit system, there are 2 trailing bits, so negative numbers and positive numbers represented by the same bit string are equivalent modulo 4. For example, 111 = -1, and 011 = 3; -1 % 4 = 3.

Knowing the underlying modular congruence relation can be useful in some fringe cases. The trick of flipping the bits and adding one doesn't work in every case. For example, if you are working with non-standard information formats, such as 24-bit integers, you may run into problems. I once had to work with a device that transmitted information stored in 24-bit integers at regular intervals. I was reading this information into a computer using a USB cable.

Unfortunately, the programming environment I was using on the computer required standard sized integers. Therefore, I had to convert the 24-bit integers into 32-bit integers. To my chagrin, all the integers were being interpreted as positive values, even though the data was actually signed voltage information.   As a result, negative numbers were being interpreted as humongous positive numbers that were way off of the scale of the graph I was trying to display.

I tried casting the data explicitly to a signed integer, but that didn't work, because by left-padding the 24-bit integers with a byte of zeros to turn them into 32-bit integers, I had made all integers look positive to the computer! Whether I cast them as signed or unsigned, they represented the same positive value because of the leading zero. Next, I tried flipping the bits and adding 1, but that also flipped the padding zeros in the leading byte into 1s while turning the last 24 bytes into a small positive number, resulting in a humongous negative number instead of the small positive number storing the magnitude of the negative number, which was what I was trying to get at.

Finally, I ended up subtracting the incoming data by 2 raised to 24, which gave me exactly the values that I needed, because the interpreter was smart enough to realize that the result should be unsigned. This worked because adding or subtracting by a particular number produces a result which has the same remainder when divided by that number. For example, -1 % 4 = 3, and -1 + 4 = 3; 7 % 4 = 3, and 7 - 4 = 3. Do you see the pattern?

Decimal Complement

Another advantage of understanding how two's complement works from a set theoretical perspective is that we can extend the concept to arbitrary number systems, such as a hypothetical decimal system in which the functional units of our computer were somehow able to store 10 distinct states. In this case, we have 10 symbols, ranging in value from 0 to 9. Consider a 2-digit decimal string. There are 100 possible values we could store, ranging from 00 to 99.

If we want to store negative numbers, we could arbitrarily decide that any number greater than or equal to 50 will actually represent a negative number. That is, if the first digit is 5,6,7,8, or 9, this represents negative sign; if the first bit is 0,1,2,3, or 4, this represents positive sign. But which positive number will, for example, 55 represent? By analogy with 2's complement, we can just subtract from 100. 100 - 55 = 45, so 55 represents -45. Another way we can think about this is by "flipping" the digits across some imaginary threshold between 4 and 5 and then adding one. Thus 55 flipped becomes 44, and 44 + 1 = 45, so 55 = -45.

Notice that in this system, because there are 10 digits, the leading digit is able to simultaneously code for sign and magnitude! Isn't that cool? Such is the power of set theory and modular arithmetic.

Principles of Machine Mathematics (Part 2 of 3)

An Guide to Two's Complement from a Set Theoretical Perspective:

Part 2

Properties of Relations

Previously, we discussed the basics of set theory and relations. Here, we will consider some interesting properties of relations. Five fundamental properties of relations are listed below:

1. Reflexivity. A relation R is reflexive on a given set S if and only if, for every element x of the set S, the ordered pair <x,x> is in the relation R. For example, the identity relation contains every pair of the form (x,x); the identity relation on the letters of the alphabet would look like this: {<A,A>, <B,B>, <C,C>, ...}. Clearly, this relation is reflexive.
2. Irreflexivity. A relation is irreflexive on a set if and only if, for every element x in a set, <x,x> is NOT in the relation. The Rock, Paper, Scissors  the Rock, Paper, Scissors victory relation discussed in part 1 is irreflexive because no choice wins against itself; instead, a tie results if both players make the same choice. Curiously, it turns out that it is possible for a relation to be neither reflexive nor irreflexive. This is the case if some elements are related to themselves, and others are not.
3. Symmetry. A relation is reflexive if and only if, for every pair <x,y> in the relation, its reflection or mirror pair <y,x> is also in the relation. The identity relation described above is symmetric, because if we swap the elements in any given ordered pair in the relation, the mirrored ordered pair is the same, so it is still in the relation.
4. Antisymmetry. A relation R is antisymmetric on a given set S if and only if, for every pair of elements <x,y> which is both in the relation and also has its mirror pair <y,x> in the relation, x = y (x and y must be the same element). For example, the Rock, Paper, Scissors victory relation discussed in part 1 is antisymmetric. Since Paper beats Rock, Rock does not beat Paper. The identity relation is also antisymmetric, because no two distinct elements are related. It turns out that a relation can be both symmetric and antisymmetric!
5. Transitivity. A relation R is transitive on a set S if and only if for every subset of three (not necessarily distinct) elements {x,y,z} from S, if <x,y> is in R and <y,z> is in R, then <x,z> must also be in R. For example, the less-than sign is transitive; any number that is less than 10 is also less than 100 because 10 is less than 10. Conversely, Rock, Paper, Scissors is often called a "non-transitive game" because although Rock beats Scissors and Scissors beats Paper, Rock does not beat Paper (even though it beats something that beats Paper).

Thanks to Jordan Kodner for correcting me after I confused reflexivity and symmetry in this section.

Equivalence Relations

An equivalence relation is a special type of relation. Any relation which is reflexive, symmetric, and transitive is considered an equivalence relation. For example, the canonical equivalence relation is the identity relation R, where a pair of elements <x,y> is in R if and only if x = y. We discussed this relation above as an example for both reflexivity and symmetry, but it turns out that it is also transitive. If x = y and y = z, then x = z.

The identity relation is not, however, the only equivalence relation. In particular, there are two other relations that are of great interest to us when discussing two's complement. The first of these is the absolute value relation on the integers:

Represented by a formula:

Represented by an infinite set of ordered pairs:

Verify for yourself that the absolute value relation is an equivalence relation because it is reflexive, symmetric, and transitive. An interesting property of equivalence relations is that the partition a set into a set of equivalence classes where every element in a particular equivalence class is equivalent with respect to that particular equivalence relation. For example, the partitioning induced on the integers by the absolute value relation is shown below, where each equivalence class is represented as a set nested inside the set of all such classes, which represents the partition:

Another type of equivalence relation of interest two us is a modular congruence relation. We say that x is congruent to y modulo z, or in mathematical notation:

This means that the remainder of x after division by z is the same as the remainder of y after division by z, which is sometimes represented by the notation:

A really simple example of this is the distinction between odd and even numbers. Odd and even numbers are the two congruence classes modulo 2; all even numbers have the same remainder (0) when divided by 2, and all odd numbers have the same remainder (1) when divided by 2.

Modular congruence relation are more complex and harder to represent in notation than the absolute value notation, so I will simply describe the modular congruence relation modulo 2 by noting that every even number is related to every other even number and every odd number is related to every other odd number, but no even number is related to any odd number, or vice versa.

Arithmetic Invariance

Invariance is a special property of equivalence relations that describes whether or not the equivalence of any two objects or elements is preserved after identical operations are performed on these "equivalent" elements. For example, the "right invariance" of equivalence relations on strings of characters is particularly useful in discussions about the regular languages. In this context, we're going to deal with a much simpler type of invariance: arithmetic invariance.

An equivalence relation is invariant with respect to a particular operation if and only if, for any two elements in the same equivalence class as each other, both of these elements remain in the same equivalence class as each other after application of the operation in question with the same arguments (if any). Note that the elements do not have to end in the same equivalence class that they started in; they just need to continue being equivalent to each other.

For example, the absolute value relation is invariant to multiplication by integers. The numbers 2 and -2 are equivalent with respect to absolute value, as are the numbers 6 and -6, which are the numbers produced by multiplying the first pair of numbers by 3.

Another way of depicting this is as follows:

However, the absolute value relation is NOT addition-invariant. Although -2 and 2 are equivalent, 5 and 1 do not have the same absolute value, so addition by 3 does not preserve the equivalence of the elements (the number 3 was chosen completely arbitrarily for sake of example in both cases).

Because the absolute value relation is not invariant to addition, it is not arithmetic invariant. Arithmetic invariance requires that an equivalence relation is invariant to all the basic arithmetic operations.

You may have learned the rules at some point that any two even numbers add up to an even number, any two odd numbers add up to an even number, any even number plus any odd number equals an even number, any even number times any even number is even, any even number times any odd number is even, and any odd number times any odd number produces an odd number. The validity of these rules shows that the modular equivalence relation modulo 2 is invariant to both addition and multiplication. In general, modular congruence relations are fully arithmetic invariant. This property will be extremely important in the next and final installment of this topic when we finally discuss the use of two's complement to store negative numbers on a computer.

TO BE CONTINUED...

Principles of Machine Mathematics (Part 1 of 3)

An Guide to Two's Complement from a Set Theoretical Perspective:

Part 1

Introduction

The ability of computers to rapidly and accurately perform extremely complex mathematical calculations is a convenience that we often take for granted. Mathematical computations are used by the computer graphics libraries that allow us to use software with graphics, such as modern video games with stunning visuals. Complex mathematical calculations are also involved in encrypting data that we send over the internet, such as credit card numbers, when performing secure online transactions such as purchases or bill payments in a way that prevents identity theft. Behind the scenes, underlying all of these seemingly magical capabilities, there lies a complex framework of carefully engineered circuits performing logical operations for our benefit.

In this post, I will attempt to demystify a small part of process by which computers perform mathematical calculation by answering a deceptively simple-sounding question: How do computers represent negative numbers?

Background: Basics of Set Theory

In order to avoid misleading and hand-wavy answers to the question of interest, we need to first explore some fundamental mathematical concepts that are extremely useful in this context. In particular, a few basic ideas from set theory are extremely valuable tools when trying to understand how math is performed on computers.

First, we need to introduce the concept of a set. A set is a mathematical abstraction for a grouping of some items. A common analogy used to describe sets is that a set is like a bag that contains some collection of objects. This is a useful analogy because it captures the essence of what a set is while also illustrating some of the more confusing properties of sets. For example, the empty set, a set which contains nothing, is denoted by the following symbol:

A set is also often denoted by curly braces; that is, the set begins with the symbol "{" and ends with the symbol "}", and the items in the set are separated by commas. Using this convention, an empty set can also be represented by:

These two symbolic representations are equivalent and interchangeable. Note, however, that the empty set is not equivalent to a set containing the empty set:

The bag analogy illustrates this nicely. Obviously, an empty bag is not physically the same thing as a bag containing another empty bag. For similar reasons, a set containing the empty set is not empty.

Not every set is empty. In fact, there are infinitely many different examples of sets that are not empty. To give an example of what one of these would look like, we can consider the set of digits that we use to represent numbers in base 10 (this set is also sometimes called the integers modulo 10):

So much for sets. Now, we need to introduce a related concept called the relation. A relation is a mathematical construct used to represent certain kinds of relationships between two sets. A relation can represented visually by graphs (often used in algebra) or arrow diagrams (often used in philosophy and logic). A relation between two sets is always a relation from one set to another set.

For example, the ASCII table (http://www.asciitable.com/), a tool widely used in programming in the convenient use cases where one does not have to fiddle with Unicode character sets, represents multiple relations in an extremely compact form. One of these relations is a relation between the integers and the letters of the alphabet. This relation can be represented by the following arrow diagram:

For a more thorough explanation of how a function is a certain type of relation, review my prior post, Relations on Pokemon. In this post, we will only discuss properties of relations that are relevant to the theory of two's complement.

One special way of looking at a relation is to consider it as mapping both to and from the same set. In some cases, this perspective comes more naturally than in others. For example, victory conditions in the classic non-transitive game Rock, Paper, Scissors can be represented by such a relation, where each item is mapped to the choice that it beats:

If you picked a given choice in the left circle above, you would win against the choice in the right circle pointed to by the arrow leading out of your choice. Another way of representing a relation is as a set of ordered pairs, where the first element in each pair is from the domain, and the second element in each pair is from the codomain. The pairs that are present in the relation are exactly those pairs of elements connected by arrows in an arrow diagram. For example, the victory conditions in the game Rock, Paper, Scissors can be represented as the following set:

Every relation has an inverse. The inverse is obtained by swapping the domain and codomain and reversing the order of the arrows, or by simply swapping the elements in each ordered pair. For example, the inverse of the victory conditions for Rock, Paper, Scissors is the set of loss conditions:

Although every relation has an inverse, not every function has an inverse, because we define the inverse of a function to be a functional relation that reverses the relationship in question.

This post introduced the basics of set theory. This topic will be continued in the next post, where we study some useful properties of relations, before we wrap up by applying set theory to the question of representing negative numbers on computers.

TO BE CONTINUED...

For The Eyes of Dogs

A dog came in the kitchen
And stole a crust of bread.
Then cook up with a ladle
And beat him till he was dead.
Then all the dogs came running
And dug the dog a tomb
And wrote upon the tombstone
For the eyes of dogs to come:
'A dog came in the kitchen ...'

- Waiting for Godot, by Samuel Becket

I have not yet actually read Waiting for Godot, but my father once sang this song to me when I was very young, and I have never forgotten it. After my initial numbness in response to the cook's shocking violence had subsided, I was overawed by the wisdom and magical prowess of the dogs in this story, who were somehow able to dispense justice by proclaiming the cook's wrongdoing in an epitaph that swallowed the story in which it was introduced, like a snake eating its own tail.

Now, as an adult, I realize that the dogs aren't meant to be real characters in a real story, and that self-similarity in literature is a trope that is not unique to Waiting for Godot. Nevertheless, because this was my first memorable exposure to self-similarity, I subconsciously associate dogs with recursion, induction, self-similarity, and other related concepts.

Today I'd like to explore how the canine magic of self-similarity can make some simple algebra infinitely more fun. Let's consider the following function:

This function contains infinitely many nested square roots. Functions of this type, although well studied, are rarely encountered in standard mathematics curricula intended to teach practical skills like the foundations of algebra or even more advanced subjects. Nevertheless, they are quite interesting. First, we will consider how to evaluate this function for a given input. For example, suppose we're given the following:

How can we solve for y?

Next, suppose that we want to find out how to generate a particular output from this function. Can we calculate an inverse for this function? That is, for some variable y, let:

Now, we want to describe some function g such that any x and y that satisfy the above equality also satisfy:

It turns out that we can achieve both of these goals by using a single, fairly simple process of substitution. The key is to realize that in the function f, the whole is equivalent to its parts. This allows us to perform the following subsitution:

This allows us to easily evaluate the function for a given input:

Actually, since y is equivalent to an expression entirely contained within a square root, y has to be positive. Therefore:

That was fairly straightforward. Using very similar steps, we can invert the function f:

Thus, the following is an inverse of f:

Notice that this makes f an actually useful function in some sense. Normally, if we were told the following:

If we were asked to solve for y, the best we could do would probably be to use the quadratic formula:

However, we can approximate the solution as follows:

We can now easily see that, as long as certain assumptions hold true (for example, x must be greater than zero), the y inside the innermost nested square root becomes less and less significant after repeated substitutions, and this expression approaches our original function f.

Before I finish this post, I would like to add the caveat that the function g described above is not the inverse of f on the real numbers. Rather, f and g are inverse functions only on a specific subset of the real numbers. Whereas the domain and range of f are both restricted to the positive numbers, the domain of g contains the negative numbers. That is, you can plug negative numbers into g and produce a real result, whereas plugging negative numbers into f produces imaginary results, and f can never produce negative results. For example, note the following (double-check by evaluating these for yourself if you want):

Whereas:

This shows in a little more detail exactly what is going on in the evaluation example we did earlier (this is why the specific negative root of -2 showed up in the process of searching for our solution for f(6) even though it was not strictly an acceptable answer).

Slightly more troubling is the fact that f and g are not even inverses on the domain of the positive real numbers, because:

Whereas:

Note that this violates the condition we stipulated earlier that x (the argument to f) must be greater than zero for the inverse relationship to hold, for the nested y does not become less significant with repeated substitutions if x is zero.

In fact, f and g are inverses on the set of positive integers greater than 1. Any such integer can be evaluated by both f and g, and f(g(x)) = x for all positive integers x greater than 1. However, this is not the largest subset of the real numbers on which f and g are inverses. There is some continuous subset of the positive real numbers on which this property holds. Interestingly, I believe that the following is also true on this subset:

However, I am not able to prove this rigorously or precisely delineate the largest subset of the real numbers on which the composition of f and g is the identity relation. I am sure somebody knows the answer, and it's probably on the internet somewhere, but I have yet to find it.

The eyes of dogs are fairly poor because dogs rely far more heavily on olfactory and auditory stimuli than on visual stimuli. Maybe for this kind of problem, it's not how you look at it that matters; maybe you have to sniff out the solution somehow. Right now, my nose just isn't good enough.

UPDATE: After asking around for help, I finally got some great advice from Tony! He pointed out that a function must converge and also be injective in order to be invertible. Note that since the graph of g(x) is a parabola, it clearly fails the vertical line test, and is not injective. To avoid confusion, I should clarify here that in this discussion I am defining g to be the function we described above:

Even though our original motivation for talking about g was finding the inverse of f, I am not defining g to be the inverse of f. Rather, let us define g to be the function above and discuss under what conditions, if any, f is the inverse of this function g.

The portion of g(x) where x is a Real number greater than one is injective and surjective onto the non-negative real numbers, since g(1) = 0 and g(x) is monotonically increasing for inputs greater than 1. That is, the g(x) is an invertible function given the following criteria:

First, g must be restricted to the domain:

This will ensure that g has the following range:

Based on my attempts to plot f(x) in Wolfram Alpha by approximation using a finite number of nestings, f appears to be injective, in fact monotonically increasing, on the nonnegative real numbers. Since we know that:

This means that f is probably surjective onto the nonnegative real numbers. Therefore, f is invertible on a different domain than g.

However, on the domain of Real numbers greater than or equal to 2, I believe that f and g are inverses of each other, because f(2) = g(2) = 2, and both f and g are monotonically increasing on this domain, meaning that they are invertible. 

Both f and g are actually invertible on larger domains then this, but in those cases they are not necessarily equal to each other's inverses. For example, it just so happens f(0) = g(0) = 0, but we know that in general g cannot be the inverse of f on the continuous interval [0,2], because g(1) = 0 and f(0) = 0. 

Therefore, there must be some other function which is in general the inverse of f on the non-negative real numbers and which is equal to g only on some subset of this domain. Similarly, there must be some function which is in general the inverse of g on the real numbers greater than or equal to 1, but which is only equal to f on some subset of this domain.

I've said "there must be" or "I believe" a lot in this blog, because I've been trying to reconcile graphical approximations from Wolfram Alpha that I used to visualize some of these functions with the properties that I know about functions and some of the more concrete algebra above. I'm not sure how confidently I can draw some of these conclusions, but I think I've settled most of the questions I wanted to answer to my satisfaction - at least, I don't have any intuition about how to proceed more rigorously. This post is definitely pushing the borders of what I actually understand about math.